由： 馬歇爾大腦

　　布爾邏輯會影響計算機的運行方式。 蒙蒂樂森/蓋蒂圖片社

　　你有沒有想過計算機如何做一些事情，比如平衡支票簿，或者 下棋，還是對文檔進行拼寫檢查?這些事情，就在幾十年前，只有人類才能做到。現在計算機顯然很容易做到。由硅和電線組成的“芯片”如何做一些看似需要人類思考的事情?

　　如果你想從最核心上理解這個問題的答案，你需要理解的第一件事是所謂的 布爾邏輯.布爾邏輯最初由喬治·布爾在 1800 年代中期開發，允許將許多意想不到的東西映射到 位和字節.布爾邏輯的偉大之處在于，一旦你掌握了竅門，布爾邏輯(或者至少是理解計算機操作所需的部分)就非常簡單。在本文中，我們將首先討論簡單的邏輯“門”，然后看看如何將它們組合成有用的東西。

　　簡易閘門

　　非門

　　和門

　　手術室門

　　諾爾門

　　您需要了解三個，五個或七個簡單的門，具體取決于您要如何計算它們(您稍后會明白為什么)。通過這些簡單的門，您可以構建組合，實現您能想象到的任何數字組件。這些門在這里看起來有點枯燥，而且非常簡單，但我們將在以下部分中看到一些有趣的組合，使它們更加鼓舞人心。如果您還沒有這樣做，請閱讀 位和字節的工作原理 在繼續之前會有所幫助。

　　非門

　　最簡單的門稱為“逆變器”或非門。它接受一個位作為輸入，并產生相反的輸出。邏輯表為：

　　一問

　　0 1

　　1 0

　　NOT 門有一個輸入，稱為 一個 和一個輸出稱為 Q (“Q”用于輸出，因為如果您使用“O”，則很容易將其與零混淆)。下表顯示了門的行為方式。將 0 應用于 A 時，Q 將生成 1。將 1 應用于 A 時，Q 會產生 0。簡單。

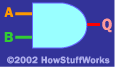
　　和門

　　AND 門對兩個輸入 A 和 B 執行邏輯“和”操作：

　　阿 乙 問

　　0 0 0

　　0 1 0

　　1 0 0

　　1 1 1

　　AND門背后的想法是，“如果 和 B 都是 1，那么 Q 應該是 1。 您可以在門的邏輯表中看到該行為。您逐行閱讀此表，如下所示：

　　阿 乙 問

　　0 0 0 如果 A 為 0，B 為 0，則 Q 為 0。

　　0 1 0 如果 A 為 0，B 為 1，則 Q 為 0。

　　1 0 0 如果 A 為 1，B 為 0，則 Q 為 0.

　　1 1 1 如果 A 為 1，B 為 1，則 Q 為 1。

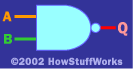
　　手術室門

　　下一個門是 OR 門。它的基本思想是，“如果 A 是 1 或 B 是 1(或兩者都是 1)，那么 Q 是 1。

　　阿 乙 問

　　0 0 0

　　0 1 1

　　1 0 1

　　1 1 1

　　南門

　　這是三個基本的門(這是計算它們的一種方法)。識別另外兩個也是很常見的： 非南 和 也不 門。這兩個門只是 AND 或 OR 門與 NOT 門的組合。如果包括這兩個門，則計數上升到五個。以下是 NAND 和 NOR 門的基本操作 - 您可以看到它們只是 AND 和 OR 門的反轉：

　　諾爾門

　　阿 乙 問

　　0 0 1

　　0 1 0

　　1 0 0

　　1 1 0

　　南門

　　阿 乙 問

　　0 0 1

　　0 1 1

　　1 0 1

　　1 1 0

　　有時添加到列表中的最后兩個門是 異或 和 XNOR 門，也稱為“獨占”和“獨占”非“門。以下是他們的表格：

　　異或門

　　阿 乙 問

　　0 0 0

　　0 1 1

　　1 0 1

　　1 1 0

　　XNOR門

　　阿 乙 問

　　0 0 1

　　0 1 0

　　1 0 0

　　1 1 1

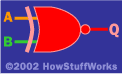
　　異或門

　　XNOR門

　　異或門背后的想法是，“如果 或 B 是 1，但 不 兩者都是，Q 是 1。 XOR 可能不包含在門列表中的原因是，您可以使用列出的原始三個門輕松實現它。

　　如果您嘗試 A 和 B 的所有四種不同模式并通過電路跟蹤它們，您會發現 Q 的行為類似于 XOR 門。由于異或門有一個很好理解的符號，因此通常更容易將異或視為“標準門”，并以與電路圖中的AND和OR相同的方式使用它。

　　簡單的加法器

　　在關于 位和字節，您了解了 二進制加法.在本節中，您將學習如何使用上一節中描述的門創建能夠進行二進制加法的電路。

　　讓我們從一個 單比特加法器.假設您有一個項目，您需要將單個位相加并獲得答案。您開始為此設計電路的方式是首先查看所有邏輯組合。您可以通過查看以下四個總和來做到這一點：

　　0 + 0 = 0

　　0 + 1 = 1

　　1 + 0 = 1

　　1 + 1 = 10

　　在你達到 1 + 1 之前，這看起來很好。在這種情況下，你有那個討厭的 進位 要擔心。如果你不關心攜帶(因為這畢竟是一個 1 位加法問題)，那么你可以看到你可以用 XOR 門解決這個問題。但是，如果您確實關心，那么您可以重寫您的方程式以始終包含 2 位輸出喜歡這個：

　　0 + 0 = 00

　　0 + 1 = 01

　　1 + 0 = 01

　　1 + 1 = 10

　　從這些等式中，您可以形成邏輯表：

　　帶外帶的 1 位加法器

　　A B Q CO

　　0 0 0 0

　　0 1 1 0

　　1 0 1 0

　　1 1 0 1

　　通過查看此表，您可以看到可以使用 XOR 門實現 Q，并使用 AND 門實現 CO(帶出)。簡單。

　　如果要將兩個 8 位字節加在一起怎么辦?這變得稍微困難一些。最簡單的解決方案是將問題模塊化為 可重復使用的組件 然后復制組件。在這種情況下，我們只需要創建一個組件：a 全二進制加法器.

　　完整加法器和我們之前查看的加法器之間的區別在于，完整加法器接受 A 和 B 輸入以及 隨身攜帶 (CI)輸入。一旦我們有一個完整的加法器，那么我們可以將其中的八個串在一起以創建一個字節寬的加法器，并將進位從一個加法器級聯到下一個加法器。

　　在下一節中，我們將了解如何在電路中實現完整的加法器。

　　全加法器

　　完整加法器的邏輯表比我們以前使用的表稍微復雜一些，因為現在我們有 3 個輸入位.它看起來像這樣：

　　具有隨身攜帶和帶出功能的一位全加法器

　　CI A B Q CO

　　0 0 0 0 0

　　0 0 1 1 0

　　0 1 0 1 0

　　0 1 1 0 1

　　1 0 0 1 0

　　1 0 1 0 1

　　1 1 0 0 1

　　1 1 1 1 1

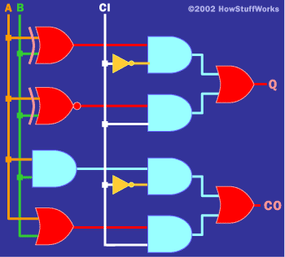
　　Full adders can be implemented in a wide variety of ways.

　　There are many different ways that you might implement this table. I am going to present one method here that has the benefit of being easy to understand. If you look at the Q bit, you can see that the top 4 bits are behaving like an XOR gate with respect to A and B, while the bottom 4 bits are behaving like an XNOR gate with respect to A and B. Similarly, the top 4 bits of CO are behaving like an AND gate with respect to A and B, and the bottom 4 bits behave like an OR gate. Taking those facts, the following circuit implements a full adder:

　　這絕對不是實現完整加法器的最有效方法，但使用此方法非常容易理解和跟蹤邏輯。如果你有這樣的傾向，看看你可以做些什么來用更少的門來實現這個邏輯。

　　現在我們有了一個叫做“完整加法器”的功能。然后，計算機工程師所做的就是“黑匣子”，這樣他或她就可以不再擔心組件的細節。一個 黑盒子 對于完整的加法器，如下所示：

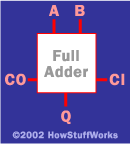
　　有了這個黑匣子，現在很容易畫一個 4 位全加法器:

　　在此圖中，每個位的進展直接饋入下一個位的進料。0 硬連接到初始進位。如果您在 A 和 B 行上輸入兩個 4 位數字，您將在 Q 行上得到 4 位總和，加上 1 個額外的位用于最終結轉。您可以看到，如果需要，該鏈可以擴展到8，16或32位。

　　我們剛剛創建的 4 位加法器稱為 紋波型進位 蝰蛇。它之所以得名，是因為進位從一個加法器到下一個加法器“紋波”。這種實現的優點是簡單，但缺點是速度問題。在實際電路中，門需要時間來切換狀態(時間在納秒量級，但在高速計算機中，納秒很重要)。因此，由于進位紋波，32 位或 64 位紋波加法器可能需要 100 到 200 納秒才能穩定到其最終總和。出于這個原因，工程師們創造了更先進的加法器，稱為 前瞻 加法 器。實現前進位所需的門數很多，但加法器的建立時間要好得多。

　　人字拖

　　使用兩個逆變器的最簡單反饋電路你可以用布爾門做的一件更有趣的事情是創建 記憶 和他們在一起。如果正確排列門，它們將記住輸入值。這個簡單的概念是 公羊 (隨機存取存儲器)在計算機中，并且還可以創建各種其他有用的電路。

　　記憶依賴于一個叫做 反饋.也就是說，門的輸出被反饋到輸入中。使用兩個逆變器的最簡單反饋電路如上所示。

　　如果遵循反饋路徑，您可以看到，如果 Q 恰好為 1，它將始終為 1。如果恰好為 0，則始終為 0。由于能夠控制我們創建的電路很好，所以這個電路沒有多大用處 - 但它確實可以讓您看到反饋的工作原理。

　　事實證明，在“真實”電路中，您實際上可以使用這種簡單的逆變器反饋方法。一個更有用的 使用兩個NAND門的反饋電路如下所示：

　　該電路有兩個輸入(R 和 S) 和兩個輸出 (Q 和 Q').由于反饋，與我們之前看到的邏輯表相比，它的邏輯表有點不尋常：

　　R S Q Q'

　　0 0 非法

　　0 1 1 0

　　1 0 0 1

　　1 1 記住

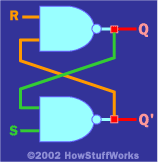
　　邏輯表顯示的是：

　　如果 R 和 S 彼此相反，則 Q 跟隨 S，Q' 是 Q 的逆。

　　如果R和S同時切換到1，則電路 記得 之前在 R 和 S 上介紹的內容。

　　還有搞笑的 非法 州。在這種狀態下，R 和 S 都變為 0，這在內存意義上沒有值。由于非法狀態，您通常會添加一點 調節邏輯 在輸入側防止它，一個此處顯示：

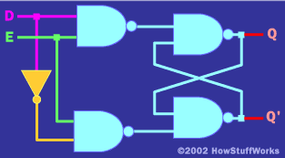
　　在該電路中，有兩個輸入(D和E)。你可以想到 D 作為“數據”和 E 如果 E 為 1，則 Q 將跟隨 D。但是，如果 E 更改為 0，Q 將記住上次在 D 上看到的內容。以這種方式運行的電路通常稱為 人字拖.

　　在下一節中，我們將介紹 J-K 觸發器。

　　J-K 人字拖

　　一種非常常見的人字拖形式是 J-K 人字拖.從歷史上看，目前尚不清楚“J-K”這個名字是從哪里來的，但它通常用這樣的黑匣子表示：

　　在此圖中， P 代表“預設”， C 代表“清除”和 時鐘 代表“時鐘”。

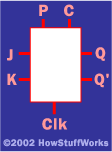
　　J-K 觸發器可用于創建和邊緣觸發鎖存，這對 CPU 的設計非常重要。

　　P C Clk J K Q Q'

　　1 1 1 比 0 1 0 1 0

　　1 1 1 比 0 0 1 0 1

　　1 1 1 1 比 0 1 1 切換

　　1 0 x x x 0 1

　　0 1 x x 1 0

　　下表是這樣說的：首先，預設和清除完全覆蓋 J、K 和 Clk。因此，如果預設變為 0，則 Q 變為 1;如果 Clear 變為 0，則無論 J、K 和 Clk 在做什么，Q 都會變為 0。但是，如果預設和清除均為 1，則 J、K 和 Clk 可以操作。這 1對0 符號意味著當時鐘從 1 變為 0 時，如果 J 和 K 的值相反，則會記住它們。在 低邊 的時鐘(從 1 到 0 的轉換)，存儲 J 和 K。但是，如果 J 和 K 恰好在低邊為 1，則 Q 只是 切換.也就是說，Q 從其當前狀態變為相反狀態。

　　你現在可能會問自己，“這到底有什么好處? 事實證明，”邊緣觸發“的概念非常有用。事實上，J-K 觸發器僅在從 1 到 0 的轉換中“鎖存”J-K 輸入，這使得它作為存儲設備更有用。J-K 人字拖在 計數器 (在以下情況下廣泛使用 創建數字時鐘).下面是一個示例 使用 J-K 觸發器的 4 位計數器:

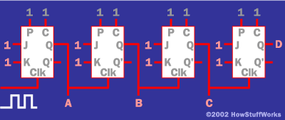
　　該電路的輸出為A、B、C和D，它們代表一個4位二進制數。在最左邊的人字拖的時鐘輸入中，有一個信號反復從 1 變為 0，然后又變回 1(一個 振蕩信號).計數器將計算它在此信號中看到的低邊沿。也就是說，每次輸入信號從 1 變為 0 時，由 A、B、C 和 D 表示的 4 位數字將遞增 1。因此，計數將從 0 變為 15，然后循環回 0。您可以向此計數器添加任意數量的位，并計算您喜歡的任何內容。例如，如果您在門上放置磁性開關，計數器將計算門打開和關閉的次數。如果你在道路上放置一個光學傳感器，計數器可以計算駛過的汽車數量。

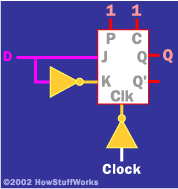
　　J-K 觸發器的另一個用途是創建一個 邊緣觸發鎖存器，如下所示。

　　在這種安排中，當時鐘邊沿從低到高時，D上的值被“鎖存”。 鎖 存 在諸如以下事物的設計中非常重要 中央處理單元 計算機中的(CPU)和外圍設備。

　　實施門

　　在前面的部分中，我們看到，通過使用非常簡單的布爾門，我們可以實現加法器、計數器、鎖存器等。這是一個巨大的成就，因為不久前，人類是唯一能夠做到將兩個數字相加的人。只要稍加努力，就不難設計出實現減法、乘法、除法的布爾電路......您可以看到，我們離袖珍計算器并不遙遠。從那里開始，跳到全面發展并不太遠 中央處理器 用于計算機。

　　那么我們如何在現實生活中實現這些門呢?布爾先生把它們寫在紙上，在紙上看起來很棒。然而，要使用它們，我們需要在物理現實中實現它們，以便門可以主動執行它們的邏輯。一旦我們實現了這一飛躍，那么我們就開始了創建真正計算設備的道路。

　　理解布爾邏輯的物理實現的最簡單方法是使用 繼 電器.事實上，這就是第一臺計算機的實現方式。沒有人再用繼電器實現計算機了——今天，人們使用蝕刻在硅芯片上的亞微觀晶體管。這些晶體管非常小且速度快，與繼電器相比，它們消耗的功率非常少。然而，繼電器非常容易理解，它們可以非常簡單地實現布爾邏輯。由于這種簡單性，您將能夠看到從“紙上的門”到“在物理現實中實現的活動門”的映射是可能且直接的。使用晶體管執行相同的映射同樣簡單。

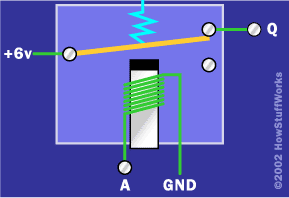
　　讓我們從逆變器開始。使用繼電器實現NOT門很容易：我們要做的是使用電壓來表示位狀態。我們將二進制 1 定義為 6 伏，將二進制 0 定義為零伏(接地)。然后我們將使用 6 伏 電池 為我們的電路供電。因此，我們的 NOT 門將如下所示：

　　[如果這個數字對你來說沒有意義，請閱讀 繼電器的工作原理 解釋一下。

　　在這個電路中，你可以看到，如果你對A施加零伏特，那么你在Q上得到6伏特;如果你對 A 施加 6 伏特，你會在 Q 上得到零伏特。實現帶繼電器的逆變器非常容易!

　　實現帶有兩個繼電器的AND門同樣容易：

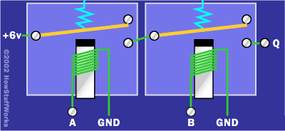
　　在這里你可以看到，如果你對 A 和 B 施加 6 伏，Q 將有 6 伏。否則，Q 的電壓為零。這正是我們想要從 AND 門獲得的行為。OR門甚至更簡單 - 只需將A和B的兩根電線連接在一起即可創建OR。如果您愿意并并行使用兩個繼電器，您可以獲得比這更華麗的東西。

　　從這個討論中可以看出，你可以從繼電器創建三個基本門——NOT、AND 和 OR。然后，您可以使用上面顯示的邏輯圖將這些物理門連接在一起，以創建物理 8 位紋波進位加法器。如果您使用簡單的開關將 A 和 B 輸入施加到加法器并將所有八條 Q 線連接到燈泡，您將能夠將任意兩個數字相加并在燈上讀取結果(“亮起”= 1，“燈熄滅”= 0)。

　　簡單門形式的布爾邏輯非常簡單。從簡單的門，您可以創建更復雜的功能，例如加法。物理實施門是可能且容易的。從這三個事實中，您擁有數字革命的核心，并且您了解計算機的核心工作原理。